

En esta página podrás encontrar problemas curiosos para los que en general no hace falta falta ninguna formación matemática previa, pero sí un cierto razonamiento lógico. Tómatelos como una especie de colección de pasatiempos. Ánimo y a por ellos. Algún día incluiré indicaciones para su resolución. De momento siempre puedes contactar conmigo para pedirme pistas, o la resolución completa. Mi dirección de correo electrónico esangbar@wmatem.eis.uva.es
Comenzamos por algo sencillito.
¿Podrías descomponer esta figura en 7 polígonos congruentes, es decir, que unos de otros difieran solamente en posibles traslaciones, rotaciones o reflexiones especulares? Nota: todas las líneas de la frontera de la figura tienen longitud 1 y los ángulos internos que aparecen son de 90, 120, 150, 210 y 240 grados.Seguimos con algo un poco más entretenido.
Considera los números 1,2,3,...,1000. Demuestra que en cualquier subconjunto con 501 de estos números siempre existen dos números tales que uno es múltiplo del otro.
Este problema perteneció a una Olimpiada Matemática.
Sea n>1 un número natural. Sea M un conjunto de intervalos cerrados. Supóngase que los eextremos u,v de cada intervalo [u,v] de M son números naturales que satisfacen 1<=u<v<=n y que dos intervalos distintos I e I', o bien tienen intersección vacía, o bien uno está contenido en el otro, es decir, dos intervalos distintos nunca se solapan parcialmente. Demuéstrese que |M|<=n-1.
Ahora un problema clásico de teoría de grafos. El famoso problema de los puentes de Königsberg.
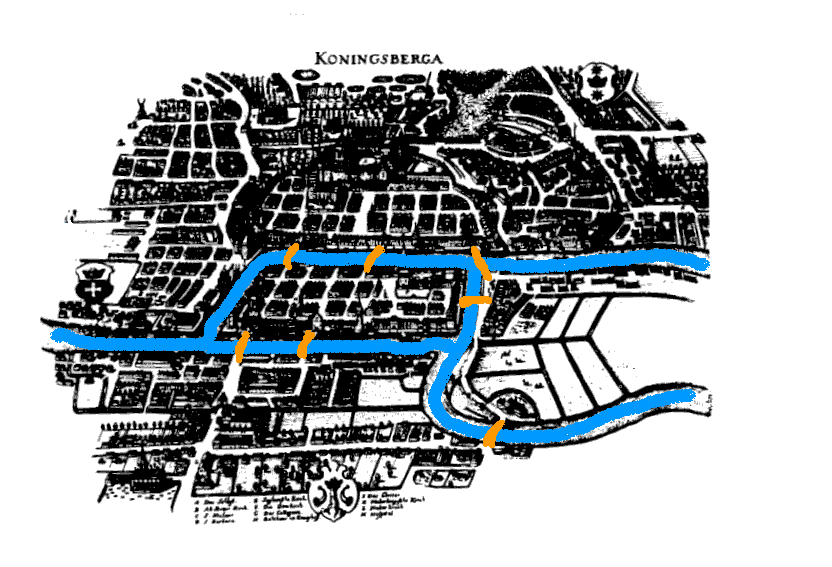
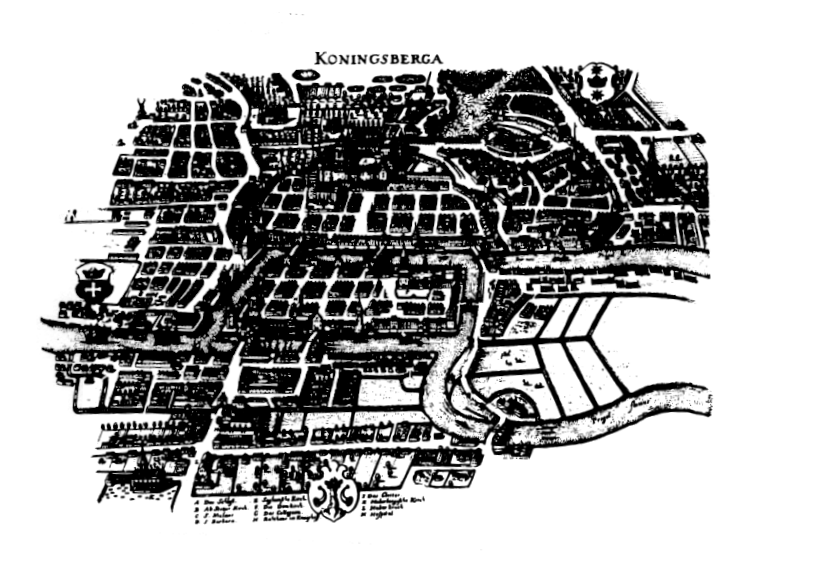
La antigua ciudad de Königsberg (hoy Kaliningrado, en Rusia) es atravesada por el río Pregel formando islas en la forma que se aprecia en el grabado.
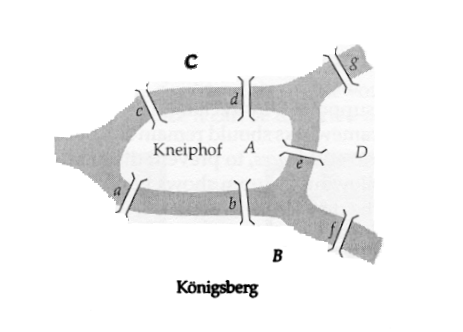
Sobre el río se han construído siete puentes en las posiciones que también se aprecian en las figuras. ¿Puede alguien dar un paseo por la ciudad atravesando todos los puentes, pero solamente una vez cada uno de ellos?
Este problema fue resuelto de forma matemática por Leonhard Euler en un artículo de 1736 que se considera como el origen de la Teoría de Grafos.
Siguiendo con el mismo tipo de problema, ¿Se puede dibujar el sobre cerrado sin levantar el lápiz y trazando casa línea una sola vez? ¿Y el sobre abierto? ¿Y la siguiente figura?
Sigamos con la teoría de grafos.
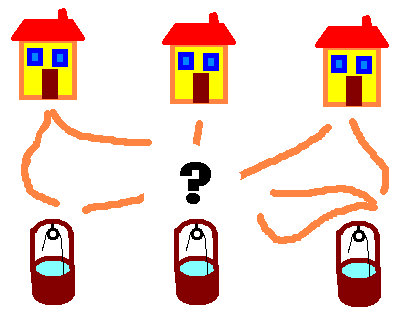
Supongamos que tres casas se abastecen de agua con tres pozos, pero los vecinos no se llevan bien y no quieren que exista la posibilidad de cruzarse con otro vecino al ir a cualquiera de los pozos. ¿Puedes diseñar caminos que unan cada casa con cada uno de los tres pozos, pero de modos que dos caminos cualesquiera nunca se cruzen entre sí? ¿Y si el planeta en que viven los tres vecinos no tuviera forma esférica?
Dejemos los grafos de momento y vamos con la geometría.¿En cuántas regiones queda dividido el plano cuando se trazan n líneas en posición general, es decir, de modo que ningún par de líneas sean paralelas y que nunca más de dos líneas intersequen en el mismo punto?
Solución: n(n+1)/2+1
Ahora nos dedicaremos a alicatar.
Sea un cuadrado formado por 2^n*2^n cuadraditos como se muestra en la figua (hemos ilustrado el caso n=3). Supongamos que se suprime uno de los cuadraditos al azar. Demuestra que la superficie que queda, cualquiera que sea el cuadradito suprimido, siempre puede ser 'alicatada' completamente con azulejos formados por tres cuadraditos en forma de L, como el que se muestra en la figura, sin que queden huecos ni se produzcan solapamientos.Indicación: Razónese por inducción.



No hay comentarios:
Publicar un comentario